Boolean Equation
Boolean Equation은 TRUE or FALSE의 변수를 다루는 방정식을 말한다. 따라서 digital logic을 묘사하기에 적절하다.
Boolean Equation에서 연산 순서는 매우 중요하다. NOT > AND > OR
1. Sum-of-Products form
N개 input에 대한 truth table은 2^N개의 행을 가진다. 그리고 각 행은 TRUE가 되는 minterm을 하나씩 가진다.
minterm은 모든 input들의 product(곱)의 형태로 나타낸 항이다.

모든 truth table에 대해 Y가 TRUE가 되는 행의 minterm을 모두 더해 Boolean equation을 작성할 수 있다. 위의 표에서는 두번째 행(A=0, B=1)일 때의 minterm을 추출해 작성할 수 있다. 이 형태를 sum-of-products canonical form 이라고 부른다.
sum-of-product의 형태는 다음과 같다.

∑를 이용해서 표현할 수도 있는데, F(A, B) = ∑(m1) 혹은 F(A, B) = ∑(1)로 표현된다.
sum-of-product form은 가장 단순한 방정식을 만들지는 않는다.
2. Product-of-Sums form
boolean function을 표현하는 또 다른 방법으로 product-of-sums canonical form이 있다.
truth table의 각 행은 FALSE가 되는 maxterm을 하나씩 가진다. maxterm은 모든 input들의 sum으로 나타낸 항이다.

모든 truth table에 대해 Y가 FALSE가 되는 행의 maxterm을 모두 더해 Boolean equation을 작성할 수 있다. 위의 표에서는 첫 번째 행과 세 번째 행에서 Y가 False가 된다. 이 두 행의 maxterm을 추출해 boolean equation을 작성한다.
π를 이용해서 표현할 수 있는데, F(A, B) = π(M0, M2) 혹은 F(A, B) = π(0, 2)로 표현된다.
product-of-sum의 형태는 다음과 같다.
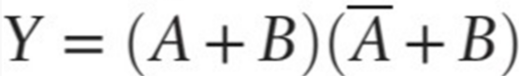
Boolean Algebra
효율성을 위해 논리 게이트의 가장 간략한 형태를 나타내는 것이 필요하다. 하지만 위에서 살펴본 두 표현은 가장 간략한 형태를 나타내는 것이 아니다. 수식을 단순화하기 위해 algebra를 사용하듯, bool equation을 단순화하기 위해 boolean algebra를 사용한다.
1. Axioms(공리)
boolean algebra는 항상 옳다고 가정하는 공리에 기초한다. 이 공리들은 당연하게 받아들이는 것이고, 증명할 수 없다.

2. Theorems of One Variable
T1에서 T5까지는 하나의 변수만을 포함하는 식의 간략화 방법을 기술한다.

3. Theorems of Several Variables
T6에서 T12까지는 하나 이상의 변수를 포함하는 방정식을 간략화하는 방법을 설명한다.

'Computer > 디지털시스템' 카테고리의 다른 글
| [논리회로] 순차 논리회로 (Sequential Logic Circuit) (1) (0) | 2024.06.06 |
|---|---|
| [논리회로] 조합 논리회로 (Combinational Logic Circuit) (3): X, Z (1) | 2024.06.06 |
| [논리회로] 조합 논리회로 (Combinational Logic Circuit) (1) (0) | 2024.06.05 |
| [FPGA] FPGA Architectures(3): Configurable Logic Block (CLB) (0) | 2024.06.03 |


