선형회귀란?
선형 회귀 모델은 다음과 같다.

θ를 모델 파라미터라고 한다.
이 식을 벡터 형태로 더 간단하게 나타낼 수 있다.

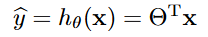
이런 수학적 notation에 익숙하지 않다면, 선형대수학을 공부하면 도움이 될 것이다.
모델을 훈련시킨다는 것은 모델이 훈련 세트에 가장 잘 맞도록 모델 파라미터를 설정하는 것이다.
여기서는 평균 제곱근 오차를 이용하고자 한다.
평균 제곱근 오차 (Root mean square error, RMSE)는 모델로 예측한 값과 실제 값의 차이를 제곱한 것을 모두 더해 평균을 구한 값이다.

RMSE는 회귀 문제의 전형적인 성능 지표이다.
이를 최소화하는 θ를 찾는 것이 모델 훈련의 목표이다.
h에 선형 회귀 모델을 적용시키면 다음과 같은 식이 도출된다.

데이터 생성
우선 선형 회귀를 테스트 하기 위한 데이터를 만들었다.
import numpy as np
np.random.seed(42)
m = 100 # 샘플 개수
X = 2 * np.random.rand(m, 1) # 열 벡터
y = 4 + 3 * X + np.random.randn(m, 1) # 열 벡터데이터의 형태를 확인해보자.
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 4))
plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()
의도한 것이지만 왠지 선형회귀를 사용하면 좋을 것 같다는 느낌이 든다.
모델 훈련
해석적인 방법으로 θ를 찾을 수 있다. 정규방정식(norm equation)을 이용하는 방법이다.

파이썬을 이용해 계산해보았다.
X_train = np.column_stack((np.ones(len(X)), X))
theta_hat = np.linalg.inv(X_train.T @ X_train) @ X_train.T @ y
theta_hat
실행 결과는 다음과 같다.
array([[4.21509616], [2.77011339]])
다음은 라이브러리를 이용해보자. Scikit-learn의 LinearRegression 클래스를 이용한다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X,y)
model.intercept_, model.coef_
실행 결과는 다음과 같다.
(array([4.21509616]), array([[2.77011339]]))
scikit-learn의 LinearRegression 클래스는 scipy.linalg.lstsq() 함수를 기반으로 한다.
이 함수는 다음 식을 계산한다.

즉, 유사역행렬(pseudoinverse)을 계산하며, 이는 특이값 분해(singular value decomposition, SVD)에 의해 이루어진다.
정규방정식과 수학적으로 동일하지만 행렬 연산을 더 효율적으로 가능하게 한다.
선형대수학에서 해당 내용을 더 자세히 공부할 수 있다.
이 함수를 이용해 구현해보자.
theta_hat_2, residuals, rank, s = np.linalg.lstsq(X_train, y, rcond=1e-6)
theta_hat_2(rcond는 cut-off condition을 생성한다. 즉, 특이값 분해(SVD)에서 작은 특이값을 무시할지 결정한다. 위 코드의 경우 특이값이 가장 큰 값의 1e-6보다 작으면 무시한다는 것을 의미한다.)
실행 결과는 다음과 같다.
array([[4.21509616], [2.77011339]])
예측 확인
위에서 구한 파라미터 값을 시각화를 통해 확인해보자.
import matplotlib.pyplot as plt
y_predict = X_train @ theta_hat
plt.plot(X, y_predict, "r-")
plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()
위의 세 예시를 통해 행렬 계산을 통해 파라미터를 최적화할 수 있으며, scikit-learn의 LinearRegression 클래스는 이러한 방식을 채택함을 알 수 있었다.
다음 글에서는 경사 하강법(gradient descent, GD)을 소개하고 이를 이용해 선형 회귀를 구현해보고자 한다.